Multi-bit CDC를 수행할 때, 동시에 여러 Bit이 Clock domain을 넘어가면 skew에 의해 전혀 다른 값이 전달될 수도 있다는 것을 알 수 있었다. 여기에서 살펴봐야 하는 점이 있다. skew에 의해 전혀 다른 값(의도와 다른 값, 예를들어 a를 b로 변경해서 전달하는데 c로 인식한 경우 의도와 다른 값이 전달.)이 전달되려면, 전달되는 Bit 중 2-bit 이상 데이터가 변경되어야 한다. 예를 들어 4-bit CDC를 수행함에 있어서, 1001 -> 1010로 변경되는 경우를 살펴보자.
[3]: 1 -> 1
[2]: 0 -> 0
[1]: 0 -> 1
[0]: 1 -> 0
위와 같이 각 BIT의 데이터 변경이 이뤄진다. 각 BIT마다 Skew가 있다고 가정하고, 이전 값을 전달하는 경우 혹은 변경된 값을 전달하는 경우로 구분하여 경우의 수를 따져보자.
[3], [2]는 데이터가 변경되지 않고 유지하므로, 그대로 [3]: 1, [2]: 0을 전달할 것이다.
[1]의 경우, 이전 값인 '0', 혹은 다음 값인 '1'을 전달할 수 있다.
[0]의 경우, 이전 값인 '1' 혹은 다음 값인 '0'을 전달할 수 있다.
각 2가지 경우를 조합하면, 4가지 경우의 수가 만들어 진다.
1. 1001 ([1]: 이전 값, [0]: 이전 값)
1. 1000 ([1]: 이전 값, [0]: 다음 값)
1. 1011 ([1]: 다음 값, [0]: 이전 값)
1. 1010 ([1]: 다음 값, [0]: 다음 값)
이와 같이 경우의 수에 따라 다른 값을 가질 수 있기 때문에 문제가 된다. 이 Multi-bit이 Counter 값이라면 어떻게 될까? 9(2'b1001) --> 10(2'b1010)으로 +1 증가하였지만, 9(2'b1001), 8(2'b1000), 11(2'b1011), 10(2'b1010)으로 이전 값을 가질 수도, 감소한 값을 전달하기도 하고, +2 증가된 값을 전달하기도 한다. 위의 예시는 4가지 경우의 수를 갖는 조건이었다. 아래 테이블과 같이 4-bit 모두 변경된다면 16가지 Case가 발생한다.

위의 내용을 정리하면, 변경되는 bit의 개수(N)가 따라 전달되는 값이 가질 수 있는 경우의 수(2^N)는 늘어나게 된다.
경우의 수를 줄이려면 변경되는 bit의 개수를 줄어야 한다. 그래서 변경되는 bit의 개수가 1개만 되도록 하는 코드가 필요하다. 그런 코드가 바로 Gray Code이다. 아래 Table은 4-bit짜리 여러 Gray code 중 reflected binary Gray code를 나타냈다.

4-bit의 값이 변경될 때 1-bit만 변경되도록 순서를 배치할 수 있다. 이렇게 되면 Clock domain을 넘어가는 값이 가질 수 있는 경우의 수는 2가지이다. 이전 값 혹은 다음 값이다. 예를 들면 0011 -> 0010으로 변경되면, 가질 수 있는 값은
0011
0010
이 2가지 경우밖에 없다. 그래서 이 코드를 사용하여 Counter를 구성하면 감소하는 경우도 없으며 +2가 되는 경우도 없다.
추가적으로 Gray Code를 구성하는 방법 중에 하나로 K-Maps을 이용하는 방법이 있다. 시작점으로부터 한칸을 이동하면 1-bit 씩 변하기 때문에 Gray Code로 생각할 수 있다.
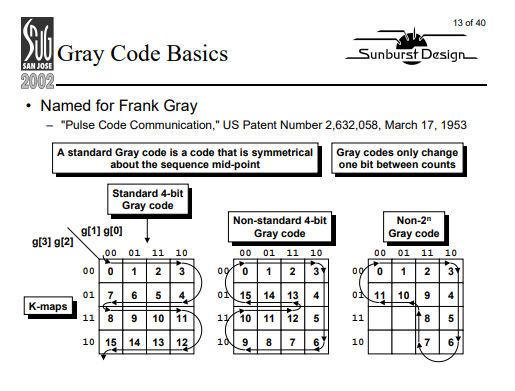
다음 포스트에서는 Gray Code 값을 이용한 Counter를 사용하기 위하여, Gray to Binary/Binary to Gray Conversion 하는 방식에 대해서 알아보겠다.
Reference
*[1]: Understanding Metastability in FPGAs, Altera Corporation
*[2]: Cummings, Clifford E. "Clock domain crossing (CDC) design & verification techniques using SystemVerilog." SNUG-2008, Boston (2008).
*[3]: S. Beer, J. Cox, T. Chaney and D. M. Zar, "MTBF Bounds for Multistage Synchronizers", 2013 IEEE 19th International Symposium on Asynchronous Circuits and Systems, 2013, pp. 158-165, doi: 10.1109/ASYNC.2013.18.
'IT_Study > ASIC_Study' 카테고리의 다른 글
| [CDC] 07. Asynchronous FIFO(1) (4) | 2022.03.29 |
|---|---|
| [CDC] 06. Gray Code vs. Binary Code(2) (5) | 2022.03.28 |
| [CDC] 04. Multi-bit Clock Domain Crossing(2) (8) | 2022.03.21 |
| [CDC] 03. Multi-bit Clock Domain Crossing(1) (4) | 2022.03.19 |
| [CDC] 02. Two Flip-flop Synchronizer Usage Example (10) | 2022.03.18 |




댓글